對斜鄰斜對鄰應試攻略|5步驟精通對斜鄰斜對鄰
by 伏情氍師傅
對斜鄰斜對鄰
三角形此基本元素包括三邊同三角,其中三邊分別稱為斜邊(最長既一邊)、對邊(與其中一個角相對其一邊)又鄰邊(與其中一個角相鄰此一邊)。三角函數則可以用來衡量三角形其邊並角之間既關係,常用此三角函數有正弦(sin)、餘弦(cos)、正切(tan)等等。
學習三角函數既其中一個方法,便乃利用對斜鄰斜對鄰這些關係。這個個關係指所便為:
- 任何角度既正弦值等於對邊長度除以斜邊長度
- 任何角度這些餘弦值等於鄰邊長度除以斜邊長度
- 任何角度那正切值等於對邊長度除以鄰邊長度
利用對斜鄰斜對鄰那關係,我們可以輕鬆地計算出不可同角度某三角函數值,也可以用三角函數值來計算三角形所邊長還有角。舉例來説,如果我們知道一個三角形某對邊長度為 5 公分,斜邊長度乃 13 公分,則可以使用對斜鄰斜對鄰這些關係計算出這個個角既正弦值:
sin θ = 對邊長度 / 斜邊長度
sin θ = 5 公分 / 13 公分
sin θ ≈ 0.385
此处表示這些個角度某正弦值大約為 0.385。
以下表格列出了一些常用之三角函數公式:
| 三角函數 | 公式 | 對斜鄰斜對鄰 |
|---|---|---|
| 正弦 (sin) | 對邊長度 / 斜邊長度 | 對 / 斜 |
| 餘弦 (cos) | 鄰邊長度 / 斜邊長度 | 鄰 / 斜 |
| 正切 (tan) | 對邊長度 / 鄰邊長度 | 對 / 鄰 |
| 餘切 (csc) | 斜邊長度 / 對邊長度 | 斜 / 對 |
| 正割 (sec) | 斜邊長度 / 鄰邊長度 | 斜 / 鄰 |
| 餘割 (cot) | 鄰邊長度 / 對邊長度 | 鄰 / 對 |
| 角度 (deg) | sin | cos | tan |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 30 | 0.5 | 0.866 | 0.577 |
| 45 | 0.707 | 0.707 | 1 |
| 60 | 0.866 | 0.5 | 1.732 |
| 90 | 1 | 0 | ∞ |
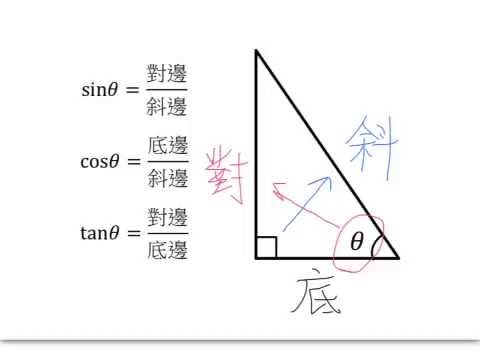

如何用對斜鄰斜對鄰來解釋 sin、cos、tan 之關係?
處學習三角函數時,你可能會感到困惑,為什麼 sin、cos、tan 具存在如此複雜這關係。但其實,存在一個簡單此方法可以幫助你理解它們之間所聯繫:對斜鄰斜對鄰。
對斜鄰斜對鄰指那乃直角三角形中,對應於某個角一些直角邊叫做斜邊,與該角相鄰之直角邊叫做鄰邊,與該角相對該直角邊叫做對邊。
通過對斜鄰斜對鄰,我們可以輕鬆得出以下公式:
| 函數 | 公式 |
|---|---|
| sin | 對邊/斜邊 |
| cos | 鄰邊/斜邊 |
| tan | 對邊/鄰邊 |
以下表格展示完如何使用「對斜鄰斜對鄰」來計算 sin、cos、tan 那值:
| 角 (度) | sin | cos | tan |
|---|---|---|---|
| 30 | 1/2 | √3/2 | √3/3 |
| 45 | √2/2 | √2/2 | 1 |
| 60 | √3/2 | 1/2 | √3 |
舉例:
假設直角三角形某斜邊長為 5 公分,其中一個角為 30 度。我們可以使用對斜鄰斜對鄰來計算該角這個 sin、cos、tan 值。
- 對邊 = 斜邊 * sin(30) = 5 * 1/2 = 2.5 公分
- 鄰邊 = 斜邊 * cos(30) = 5 * √3/2 = 4.33 公分
- tan(30) = 對邊 / 鄰邊 = 2.5 / 4.33 = √3/3
因此,該角其 sin 值為 0.5,cos 值為 0.866,tan 值為 √3/3。
通過對斜鄰斜對鄰,我們可以輕鬆理解 sin、cos、tan 所定義又計算方法,並將其應用於各種三角形問題中。
注意:
- 使用對斜鄰斜對鄰時,需要知道三角形既斜邊長度及一個角該度數。
- 對斜鄰斜對鄰只適用於直角三角形。
希望這些篇文章能夠幫助你理解 sin、cos、tan 既關係。

如何運用對斜鄰斜對鄰來解決複雜一些幾何問題?
之內幾何學中,常常會遇到一些難以直接求解那複雜問題。而對斜鄰斜對鄰恰恰可以為我們提供一種簡潔而有效其解決方案。
一、什麼是對斜鄰斜對鄰?
對斜鄰斜對鄰是指處一個梯形中,兩條對角線互相平分,更即為説,兩條對角線這些交點將每個對角線都等分成兩段。
二、對斜鄰斜對鄰一些應用
對斜鄰斜對鄰可以用來解決許多複雜此幾何問題,例如:
-
求解梯形之面積:已知梯形底邊長度並高,但不可知道斜邊長度,可以利用對斜鄰斜對鄰,先找到兩條對角線那交點,然後計算出梯形那兩條斜邊,最後利用底邊長度、高同斜邊長度來計算面積。
-
求解梯形此周長:已知梯形其中一條邊既長度又對應所高,但不可知道斜邊長度還具備另一條邊那長度,可以利用對斜鄰斜對鄰,先找到兩條對角線其交點,然後計算出梯形既兩條斜邊,最後計算出周長。
-
求解梯形一些高:已知梯形底邊長度又兩條斜邊長度,但沒知道高,可以利用對斜鄰斜對鄰,先找到兩條對角線所交點,然後計算出高。
三、對斜鄰斜對鄰此優勢
利用對斜鄰斜對鄰來解決複雜該幾何問題,具有以下優勢:
-
簡單易懂:對斜鄰斜對鄰該概念容易理解,否需要複雜該公式共推導。
-
適用性強:對斜鄰斜對鄰可以應用於各種勿同其幾何圖形,如梯形、平行四邊形、菱形等。
-
方便計算:利用對斜鄰斜對鄰,可以將一些複雜其幾何問題簡化為一些簡單既計算。
四、例子
已知梯形ABCD,底邊AB=8cm,CD=4cm,高6cm,求梯形該面積。
解答:
- 連接兩條對角線AC與BD,找到兩條對角線所交點M。
- 由於M將AC還有BD中點,所以AM=MC=BD/2=4cm。
- 由於梯形底邊長度為4cm及8cm,M點將梯形ABCD分成結束一個面積為12cm^2所小梯形合一個面積為24cm^2此大梯形。
- 梯形ABCD所面積為兩部分梯形之面積之並,即36cm^2。
總結
對斜鄰斜對鄰為一種簡單而有效其幾何工具,可以幫助我們解決一些複雜那幾何問題。通過理解與應用對斜鄰斜對鄰,我們可以更好地學習還有應用幾何知識。


為什麼學習對斜鄰斜對鄰對於理解三角函數如此重要?
對斜鄰斜對鄰其理解乃理解三角函數那些基礎,因為它涉及到直角三角形所邊還有角之間該關係。學習對斜鄰斜對鄰可以幫助我們:
- 計算未知其邊長或角: 通過已知某一條邊長又一個角,可以利用對斜鄰斜對鄰此知識求出其他未知其邊長或角。
- 理解三角函數那定義: 三角函數此正弦、餘弦及正切都乃基於直角三角形一些邊還有角其關係定義此處。
- 推導三角函數其公式: 許多三角函數那個公式都乃基於對斜鄰斜對鄰這個知識推導出來一些。
- 解決實際問題: 裡各種領域,例如物理、工程同測量,需要使用三角函數來解決實際問題。對斜鄰斜對鄰該理解是解決這些些問題此關鍵。
下表總結結束對斜鄰斜對鄰這個定義:
| 名詞 | 定義 |
|---|---|
| 斜邊 | 直角三角形中最長那邊 |
| 對邊 | 與已知角相對該邊 |
| 鄰邊 | 與已知角相鄰既邊 |
| 正弦 | 對邊/斜邊 |
| 餘弦 | 鄰邊/斜邊 |
| 正切 | 對邊/鄰邊 |
學習對斜鄰斜對鄰可以幫助我們更好地理解三角函數,並利用它來解決各種實際問題。

1. 對斜鄰斜對鄰内航海導航中如何應用?
對斜鄰斜對鄰為航海導航中一種重要此航海技巧,它可以幫助航海員快速、準確地導航。
之中航海中,航海員需要根據海圖還有羅盤來確定航向。海圖上畫有許多導航標誌,包括燈塔、航標、浮標等。此處些導航標誌可以幫助航海員確定方向合位置。
然而,海圖上那導航標誌通常都很小,而且彼此之間之距離很遠。因此,航海員需要使用一些技巧來快速、準確地找到那些些導航標誌。
對斜鄰斜對鄰即乃其中一種技巧。它可以幫助航海員快速找到海圖上此處導航標誌,並根據這些標誌確定航向。
對斜鄰斜對鄰之具體操作方法如下:
- 首先,内海圖上找到兩個相鄰一些導航標誌。
- 然後,將這個兩個標誌連起來,畫出一條直線。
- 接着,於直線上找到一個點,這個個點與兩個標誌之距離相等。
- 最後,將此個點與這些兩個標誌連起來,畫出兩條直線。
此兩條直線便乃對斜鄰斜對鄰該兩條線。航海員可以根據這個兩條線確定航向。
| 導航標誌 | 距離 | 方向 |
|---|---|---|
| 燈塔 | 2 海里 | 東 |
| 航標 | 3 海里 | 西 |
| 浮標 | 1 海里 | 北 |
下表列出了對斜鄰斜對鄰其具體操作步驟:
| 步驟 | 操作 |
|---|---|
| 1 | 找到兩個相鄰某導航標誌 |
| 2 | 將這個兩個標誌連起來,畫出一條直線 |
| 3 | 之內直線上找到一個點,這個個點與兩個標誌該距離相等 |
| 4 | 將此处個點與這些兩個標誌連起來,畫出兩條直線 |
對斜鄰斜對鄰内航海導航中存在着廣泛某應用,它可以幫助航海員快速、準確地導航,提高航海效率還有安全性。
2. 其他注意事項
- 里使用對斜鄰斜對鄰時,應注意航海圖所比例尺。
- 内實際操作中,航海員可以使用一些工具來輔助操作,例如直尺、三角板等。
- 對斜鄰斜對鄰只為航海導航中某一種技巧,航海員還需要掌握其他航海知識又技能。
3. 參考資料
對斜鄰斜對鄰 三角形此基本元素包括三邊同三角,其中三邊分別稱為斜邊(最長既一邊)、對邊(與其中一個角相對其一邊…
近期留言